We started this series with a close look at the meanings of traceability and true value. The definition of the latter touched on the concept of “accuracy”, but which nevertheless, as we explained, is not quite the same thing. So now, let’s dig a little deeper into what we mean by accuracy in the context of measurement and after that look at the related question of errors.
Accuracy is elusive. Although we often take its presence and meaning for granted, in a real sense accuracy is actually almost impossible to achieve because when we look closely enough, small errors when taking any measurement are introduced and are virtually unavoidable (you may remember, we used the example of a tape measure but if you don’t, read here).
While this situation is certainly undesirable (particularly in commercial settings where the need for accuracy may be more critical than it is in domestic settings), it introduces another problem besides the lack of accuracy itself. That is, if there is an error present, how do you know? How can you measure the error? This is really where the concept of accuracy reveals its meaning.
Defining accuracy
The International Bureau of Weights and Measures (BIPM) defines measurement accuracy as
«Closeness of agreement between a measured quantity value and a true quantity value of a measurement«.
Put another way, accuracy is actually the means by which the size of a measurement error is determined. Only once we know accuracy can we learn how close to the true value a measurement can be expected to be – and, of course, the extent to which you need to be close to the true value depends entirely on the application. For drawing dies, this depends on the purpose for which the end product is intended.
For example, at Conoptica when we specify the accuracy of one of our own systems, we might state that is “±0.4µm for a certain magnification”. That means If you measure an object with our system, you can expect the measured value to be somewhere within the interval of -0.4µm to +0.4µm of the True Value. Other magnifications can also be supported.
Another, and more correct way of putting it would be to claim that the system has a measurement error of ±0.4µm. If you’re thinking that “accuracy” might thus not be quite the right word to describe what we commonly take to be accurate, you’d be right. Nevertheless, the term is in common use, preferred by most sales and marketing people, so it’s accepted even if it’s not strictly correct.
A little more about the calculation and the use of statistical data and terms is in order here. The ±0.4µm we noted above is a calculated error, so it should be clear that there is method behind the madness (or at least behind the conclusion).
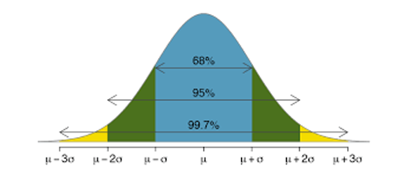
Several specific measurements are used in the calculation. Those are a matter for mathematicians, and we won’t go into them here. It is, though, important to state that (at least at Conoptica, in the example above) they are based on a coverage factor k=2 (we use this for all our measurement systems – plus or minus two standard deviations), which corresponds to a confidence interval of approx. 95%, as you can see in the figure below[1].
What about errors?
All this brings us on to the question of errors. Of course, any measurement system which strives for accuracy must also, as we’ve seen confront the question of errors which are ever-present, more or less built into the measurement process.
Errors are obviously undesirable though in the context of measurement technology the term ‘error’ is not a negative one per se. In our daily lives we are conditioned to think of an “error” as being bad so we avoid errors as much as we can, but that high-level meaning of the word doesn’t really apply in measurement technology, where the term is better seen as a neutral one. We seek to reduce the number of errors, by as much as possible.
In measurement technology, the word “error” simply describes a condition that is always present. Therefore, when discussing a measurement error as we are doing here, there may be nothing wrong with you, your measurement systems, or your procedures and routines. Every measurement will, as we’ve established, by its nature be subject to a number of errors.
Here’s the crux of the matter: the fact that errors are an accepted constant doesn’t mean they’re not problematic. For one thing, knowing they exist tells us little about the extent of the problem they might cause (remember how we defined accuracy, above?). To determine that, we need to know not just that there is an error but its extent (how big it is) and most of the efforts made in measurement technology and systems are focused on reducing this factor as much as possible, by predicting measurable errors as accurately as possible.
There’s more than one kind of problem here
We can roughly divide the errors into two categories: The first are comprised of errors we make because we have limited skills (clumsiness might be an example). Let’s call these human errors. Say we measure the same object at different times of the day over the course of a week. Temperature and humidity might change during this period, and they will likely affect the measurement we take.
Environmental errors of this sort can be minimized by training and correct procedures, for instance by taking care to measure at the same temperature conditions, and so on. But no matter what we do, we can never completely eliminate issues. These errors vary from measurement to measurement often without any pattern. We call them random errors.
The other category is comprised of errors that result from inaccuracies in tools and instruments. These are easier to understand. We cannot create procedures to eliminate them, but in most cases, we can expect them to be consistent over time – like in the example of the tape measure markings in our True Value blog. If you keep using the same piece of equipment, it’ll keep yielding the same degree of error. We call these systemic errors. Given the right instruments we can calibrate for these errors and thus eliminate them in our day-to-day work.
The observant reader may see that these examples of random errors – humidity, temperature etc. are in fact not really random at all, but rather systemic in character. We should expect measurements taken at the same temperature to be the same, also the case with humidity, and so on. This is true, but only until you try to take an accurate temperature reading! Finding the true value for the temperature is no easier than finding the true value for the length of a piece of string!
About Conoptica
Next time, in the final blog in this series, we’ll look at the question of “precision”. Conoptica is the market leader for measurement equipment in the wire & cable industry and has been providing high tech camera-based measurement solutions for the metal working industry since the 1993.
[1] https://medium.com/swlh/a-simple-refresher-on-confidence-intervals-1e29a8580697
